Appendix B — Straight Line Review

In this section we give some examples of straight lines and also look at the interpretation of slope.

Since we will use straight lines to model data when there is a trend (This is called regression) it is important that we understand what slopes mean and what the equations look like for different lines.

For slopes:

• a positive slope means increasing or uphill trend
• a negative slope means decreasing or downhill trend

Here are some examples:

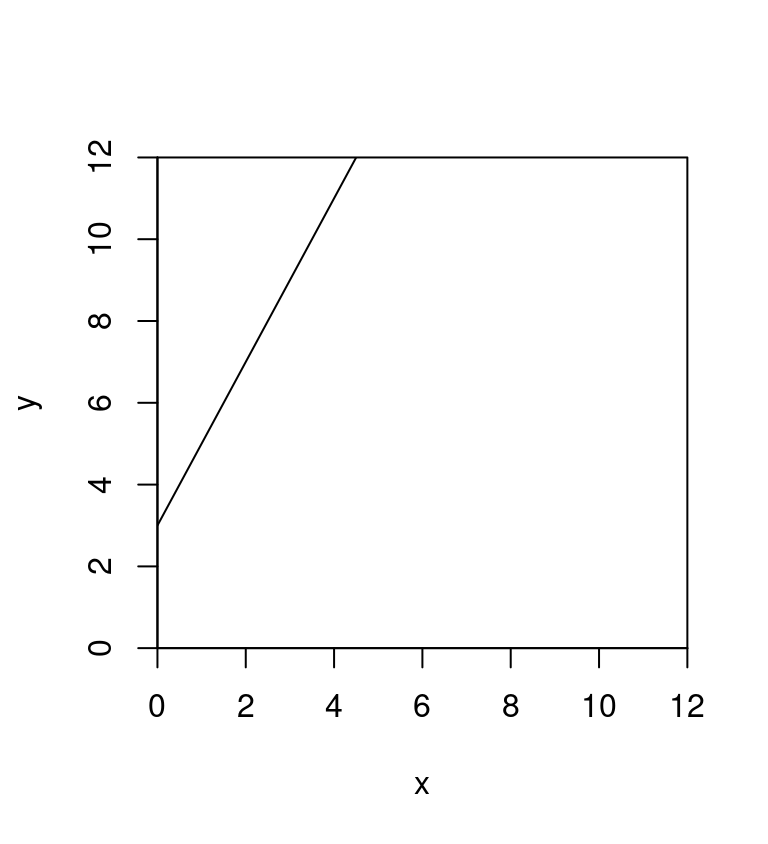
Example 1

The equation is:

\(y = 2x + 3\)

• The slope is: \(m = 2\)
• intercept is: \(b= 3\)

Interpretation of slope

For each additional unit of x, there is an increase of 2 units of y

Example 2

The equation is:

\(y = -1x + 5\)

• The slope is: \(m = -1\)
• intercept is: \(b= 5\)

Interpretation of slope

For each additional unit of x, there is an decrease of 1 units of y

Example 3

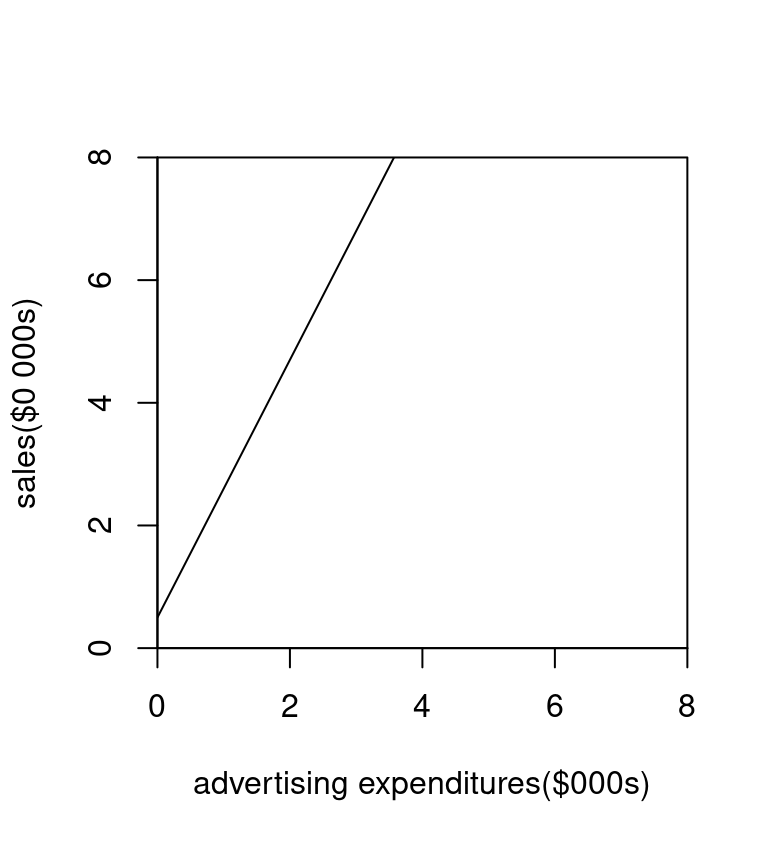
The equation is:

\(y = 2.1x + 0.5\)

• The slope is: \(m = 2.1\)
• intercept is: \(b= 0.5\)

Units

Suppose \(x\) = advertising expenditures (in $000s, so thousands of $)
Suppose \(y\) = sales (in $0 000s, so in ten thousands of $)

• So if \(x = 1.2\) that stands for $1200
  
• If \(y = 5.6\) that stands for $56,000

Interpretation of slope

For each additional unit of x (so each additional $1000 dollars spent on ads), there is an increase of 2.1 units of y (so an increase of $21,000 in sales)