This section shows how to use a spreadsheet to find left tail areas. Usually you will use something like Excel or Google Spreadsheets. They both work the same for all the calculations we show. You can use either one.
This is an alternative way to find the same areas as when we used a standard normal table in the last section.
Left Tail Areas With Spreadsheets
So here are a two examples of finding left tail area using a spreadsheet:
Example 17.1 (Left tail area for \(z=-1.02\) using spreadsheet)
Find the left tail area when \(z=-1.02\) using a spreadsheet calculation.
Solution:
We have \(z = -1.02\).
Here is the picture of the area we want.
We want the shaded region to the left of \(z=-1.02\). We will calculate this area using a spreadsheet and the NORMSDIST function which gives left tail areas for z-values.
- Type z in cell B2
- Then type \(-1.02\) into C2
- Then type in left tail area in B3,
- In cell C3 type =NORMSDIST( then click on C2 then type ) then hit enter
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
-1.02 |
|
| 3 |
|
left tail area |
=NORMSDIST(C2) |
|
| 4 |
|
|
|
|
After hitting enter you should see the result as follows:
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
-1.02 |
|
| 3 |
|
left tail area |
0.1539 |
|
| 4 |
|
|
|
|
Rounded to the nearest percent this is 15%.
This means that the left tail area for \(z=-1.02\) is 15%.
\[
\tag*{$\blacksquare$}
\]
:::{#exm-Left-tail-area-for-z-equals-1.79-using-spreadsheet} ## Left tail area for \(z=1.79\) using spreadsheet
Find the left tail area when \(z=1.79\) using a spreadsheet calculation.
Solution:
We have \(z = 1.79\).
Here is the picture of the area we want.
We want the shaded region to the left of \(z=1.79\). We will calculate this area using a spreadsheet and the NORMSDIST function which gives left tail areas for z-values.
- Type z in cell B2
- Then type \(1.79\) into C2
- Then type in left tail area in B3,
- In cell C3 type =NORMSDIST( then click on C2 then type ) then hit enter
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
1.79 |
|
| 3 |
|
left tail area |
=NORMSDIST(C2) |
|
| 4 |
|
|
|
|
After hitting enter you should see the result as follows:
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
1.79 |
|
| 3 |
|
left tail area |
0.9633 |
|
| 4 |
|
|
|
|
Rounded to the nearest percent this is 96%.
This means that the left tail area for \(z=1.79\) is 96%.
\[
\tag*{$\blacksquare$}
\]
Right Tail Areas With Spreadsheets
And here are two examples of finding the right tail area using a spreadsheet:
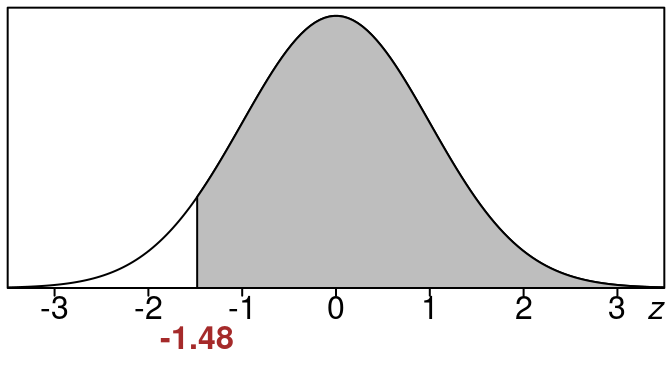
Example 17.2 (Right tail area for \(z=-1.48\) using spreadsheet)
Find the right tail area when \(z=-1.48\) using a spreadsheet calculation.
Solution:
We have \(z = -1.48\).
Here is the picture of the area we want.
We want the shaded region to the right of \(z=-1.48\).
We will calculate this area using a spreadsheet and the NORMSDIST function but because NORMSDIST finds left tails we have to use a trick. We actually will find the left tail area for this z-value, then subtract from 1.0 to get our right tail area.
- Type z in cell B2
- Then type \(-1.48\) into C2
- Then type in right tail area in B3,
- In cell C3 type =1.0-NORMSDIST( then click on C2 and then type ) then hit enter
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
-1.48 |
|
| 3 |
|
right tail area |
=1.0-NORMSDIST(C2) |
|
| 4 |
|
|
|
|
After hitting enter you should see the result as follows:
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
-1.48 |
|
| 3 |
|
right tail area |
0.9306 |
|
| 4 |
|
|
|
|
Rounded to the nearest percent this is 93%.
This means that the right tail area for \(z=-1.48\) is 93%.
\[
\tag*{$\blacksquare$}
\]
Example 17.3 (Right tail area for \(z=0.31\) using spreadsheet)
Find the right tail area when \(z=0.31\) using a spreadsheet calculation.
Solution:
We have \(z = 0.31\).
Here is the picture of the area we want.
We want the shaded region to the right of \(z=0.31\).
We will calculate this area using a spreadsheet and the NORMSDIST function but because NORMSDIST finds left tails we have to use a trick. We actually will find the left tail area for this z-value, then subtract from 1.0 to get our right tail area.
- Type z in cell B2
- Then type \(0.31\) into C2
- Then type in right tail area in B3,
- In cell C3 type =1.0-NORMSDIST( then click on C2 and then type ) then hit enter
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
0.31 |
|
| 3 |
|
right tail area |
=1.0-NORMSDIST(C2) |
|
| 4 |
|
|
|
|
After hitting enter you should see the result as follows:
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z |
0.31 |
|
| 3 |
|
right tail area |
0.3783 |
|
| 4 |
|
|
|
|
Rounded to the nearest percent this is 38%.
This means that the right tail area for \(z=0.31\) is 38%.
\[
\tag*{$\blacksquare$}
\]
Area Between With Spreadsheets
And here is an example of finding the area between using a spreadsheet:
Example 17.4 (Area between \(z1=-0.54\) and \(z2=1.24\) using spreadsheet)
Find the area between \(z_{1}=-0.54\) and \(z_{2}=1.24\) using a spreadsheet calculation.
Solution:
Here is the picture of the area we want.
We want the shaded region to the left of \(z_2=1.24\) and to the right of \(z_1 = -0.54\)
We will calculate this area using a spreadsheet and the NORMSDIST function.
Since NORMSDIST gives us left tails we look up the left tail area for the greater z-value \(z_2\) and subtract the left tail area for the lesser z-value \(z_1\).
- Type z1 in cell B2
- Then type \(-0.54\) into C2
- Type z2 in cell B3
- Then type \(1.24\) into C3
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z1 |
-0.54 |
|
| 3 |
|
z2 |
1.24 |
|
| 4 |
|
|
|
|
| 5 |
|
|
|
|
- Then type in area between in B4,
- In cell C4 enter =NORMSDIST(C3)-NORMSDIST(C2), and then hit enter
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z1 |
-0.54 |
|
| 3 |
|
z2 |
1.24 |
|
| 4 |
|
area between |
=NORMSDIST(C3)-NORMSDIST(C2) |
|
| 5 |
|
|
|
|
After hitting enter you should see the result as follows:
|
A |
B |
C |
D |
| 1 |
|
|
|
|
| 2 |
|
z1 |
-0.54 |
|
| 3 |
|
z2 |
1.24 |
|
| 4 |
|
area between |
0.5979 |
|
| 5 |
|
|
|
|
Rounded to the nearest percent this is 60%.
This means that the shaded area corresponds to 60% of the entire data.
\[
\tag*{$\blacksquare$}
\]