This section shows how to use the standard normal table to find left tail areas. We will be finding the areas for examples like these.
The standard normal table (z-table) we use is in Appendix A This table contains only left tail areas in it, so in this section we concentrate on showing examples of finding left tail area using the table.
If you have a right tail area or area between that you need to find, you will have to use some tricks to find the area you want by using the table and some left tail area. In Standard Normal Areas we see how to do that.
So here are a few examples of finding left tail areas using the table:
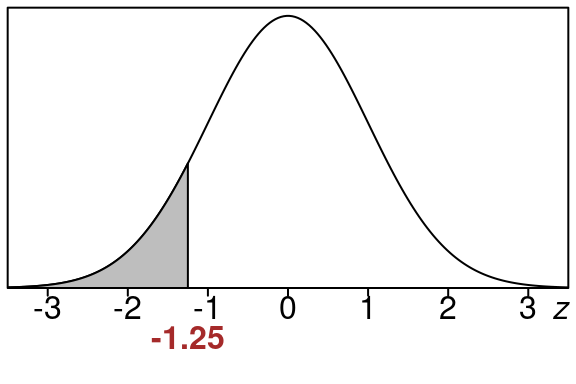
Example 15.1 (Left tail area for \(z=-1.25\))
Find the left tail area when \(z=-1.25\). Use the standard normal table.
Solution:
We have \(z=-1.25\).
Below is a picture of the area. We want to know how big the shaded area is. In particular if the whole area under the curve is 100%, how big is the shaded part?
We start by going to the row that has \(z=-1.2\) and then we go over to the column that is \(.05\). The left tail area is where the row and column meet.
|
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
| -1.5 |
.0668 |
.0655 |
.0643 |
.0630 |
.0618 |
.0606 |
.0594 |
.0582 |
.0571 |
.0559 |
| -1.4 |
.0808 |
.0793 |
.0778 |
.0764 |
.0749 |
.0735 |
.0721 |
.0708 |
.0694 |
.0681 |
| -1.3 |
.0968 |
.0951 |
.0934 |
.0918 |
.0901 |
.0885 |
.0869 |
.0853 |
.0838 |
.0823 |
| -1.2 |
.1151 |
.1131 |
.1112 |
.1093 |
.1075 |
.1056 |
.1038 |
.1020 |
.1003 |
.0985 |
| -1.1 |
.1357 |
.1335 |
.1314 |
.1292 |
.1271 |
.1251 |
.1230 |
.1210 |
.1190 |
.1170 |
| -1.0 |
.1587 |
.1562 |
.1539 |
.1515 |
.1492 |
.1469 |
.1446 |
.1423 |
.1401 |
.1379 |
| -0.9 |
.1841 |
.1814 |
.1788 |
.1762 |
.1736 |
.1711 |
.1685 |
.1660 |
.1635 |
.1611 |
So we have this: \[\begin{equation}
\text{left tail area} =0.1056
\end{equation}\]
Rounded to the nearest percent this is \(11\)%. The shaded region represents about \(11\)% of the entire area.
\[
\tag*{$\blacksquare$}
\]
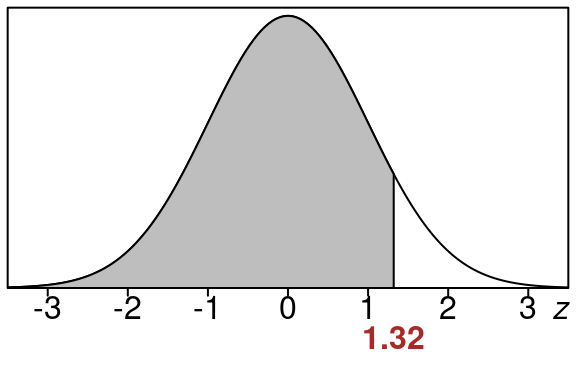
Example 15.2 (Left tail area for \(z=1.32\))
Find the left tail area when \(z=1.32\). Use the standard normal table.
Solution:
We have \(z=1.32\).
Below is a picture of the area. We want to know how big the shaded area is. In particular if the whole area under the curve is 100%, how big is the shaded part?
We start by going to the row that has \(z=1.3\) and then we go over to the column that is \(.02\). The left tail area is where the row and column meet.
|
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
| 1.0 |
.8413 |
.8438 |
.8461 |
.8485 |
.8508 |
.8531 |
.8554 |
.8577 |
.8599 |
.8621 |
| 1.1 |
.8643 |
.8665 |
.8686 |
.8708 |
.8729 |
.8749 |
.8770 |
.8790 |
.8810 |
.8830 |
| 1.2 |
.8849 |
.8869 |
.8888 |
.8907 |
.8925 |
.8944 |
.8962 |
.8980 |
.8997 |
.9015 |
| 1.3 |
.9032 |
.9049 |
.9066 |
.9082 |
.9099 |
.9115 |
.9131 |
.9147 |
.9162 |
.9177 |
| 1.4 |
.9192 |
.9207 |
.9222 |
.9236 |
.9251 |
.9265 |
.9279 |
.9292 |
.9306 |
.9319 |
| 1.5 |
.9332 |
.9345 |
.9357 |
.9370 |
.9382 |
.9394 |
.9406 |
.9418 |
.9429 |
.9441 |
| 1.6 |
.9452 |
.9463 |
.9474 |
.9484 |
.9495 |
.9505 |
.9515 |
.9525 |
.9535 |
.9545 |
So we have this: \[\begin{equation}
\text{left tail area} =0.9066
\end{equation}\]
Rounded to the nearest percent this is \(91\)%. The shaded region represents about \(91\)% of the entire area.
\[
\tag*{$\blacksquare$}
\]
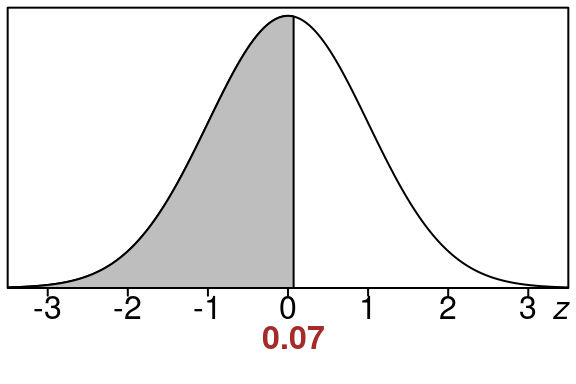
Example 15.3 (Left tail area for \(z=0.07\))
Find the left tail area when \(z=0.07\). Use the standard normal table.
Solution:
We have \(z=0.07\).
Below is a picture of the area. We want to know how big the shaded area is. In particular if the whole area under the curve is 100%, how big is the shaded part?
We start by going to the row that has \(z=0.0\) and then we go over to the column that is \(.07\). The left tail area is where the row and column meet.
|
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
| -0.2 |
.4207 |
.4168 |
.4129 |
.4090 |
.4052 |
.4013 |
.3974 |
.3936 |
.3897 |
.3859 |
| -0.1 |
.4602 |
.4562 |
.4522 |
.4483 |
.4443 |
.4404 |
.4364 |
.4325 |
.4286 |
.4247 |
| -0.0 |
.5000 |
.4960 |
.4920 |
.4880 |
.4840 |
.4801 |
.4761 |
.4721 |
.4681 |
.4641 |
| 0.0 |
.5000 |
.5040 |
.5080 |
.5120 |
.5160 |
.5199 |
.5239 |
.5279 |
.5319 |
.5359 |
| 0.1 |
.5398 |
.5438 |
.5478 |
.5517 |
.5557 |
.5596 |
.5636 |
.5675 |
.5714 |
.5753 |
| 0.2 |
.5793 |
.5832 |
.5871 |
.5910 |
.5948 |
.5987 |
.6026 |
.6064 |
.6103 |
.6141 |
| 0.3 |
.6179 |
.6217 |
.6255 |
.6293 |
.6331 |
.6368 |
.6406 |
.6443 |
.6480 |
.6517 |
So we have this: \[\begin{equation}
\text{left tail area} =0.5279
\end{equation}\]
Rounded to the nearest percent this is \(53\)%. The shaded region represents about \(53\)% of the entire area.
\[
\tag*{$\blacksquare$}
\]