| x | y |
| 16 | 45 |
| 17 | 56 |
| 18 | 58 |
| 19 | 58 |
| 20 | 75 |
28 Using the ToolPak for Regression Modeling
28.1 The Data
Lets run a regression analysis using the data analysis ToolPak. This add-in is called the Excel Analysis ToolPak in Excel. For Google Sheets it is called the XLMiner Analysis ToolPak. They both work the same way and produce similar output. The links show how to install these tools.
Here is the data we will work with for our analysis:
Here is a scatterplot of this data:
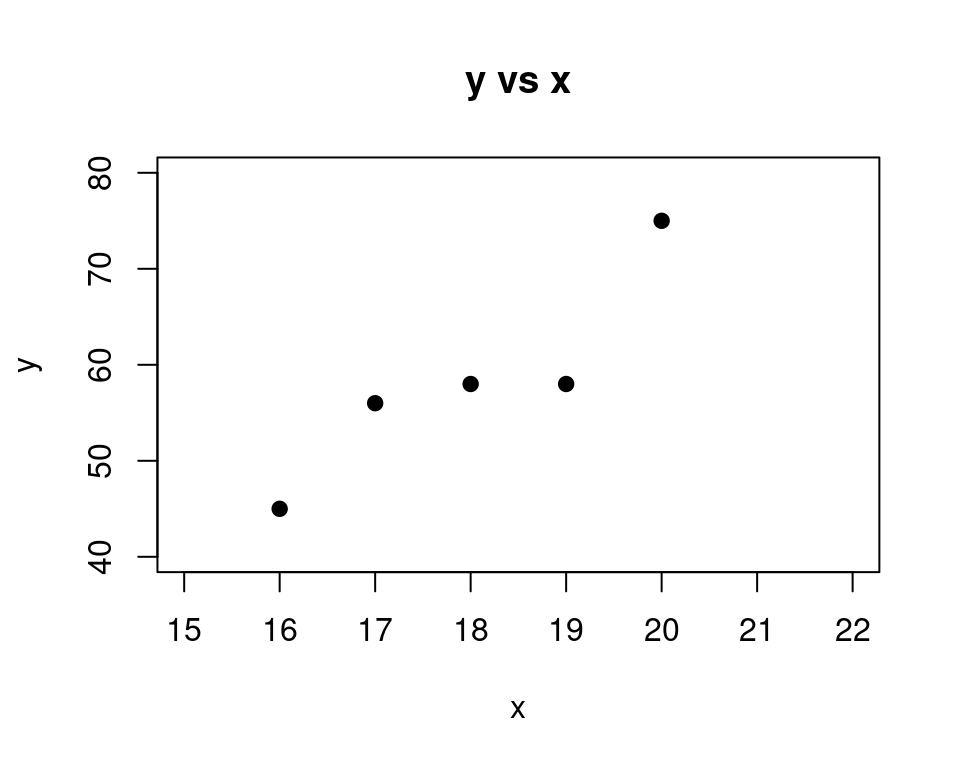
Make sure this data is entered into a spreadsheet in columns A and B of the spreadsheet. Include the names “x” and “y” in the first row as well. These are the sometimes called the labels for the variables.
| A | B | C | D | E | F | |
| 1 | x | y | ||||
| 2 | 16 | 45 | ||||
| 3 | 17 | 56 | ||||
| 4 | 18 | 58 | ||||
| 5 | 19 | 58 | ||||
| 6 | 20 | 75 | ||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 |
28.2 ToolPak Output
Run the Tookpak add-in and select the linear regression tool. For “Input Y Range” enter in B1:B6 and A1:A6 for “Input X Range”.
You can click on the “Labels” option since you have included row 1 and this contains the labels “x” and “y” for your data.
Now choose D2 as the output cell. This is where your regression summary will go. Go ahead and run the analysis and it should output something like this:
| A | B | C | D | E | F | G | H | I | J | |
| 1 | x | y | ||||||||
| 2 | 16 | 45 | Summary | |||||||
| 3 | 17 | 56 | ||||||||
| 4 | 18 | 58 | Regression | |||||||
| 5 | 19 | 58 | Multiple R | 0.913 | ||||||
| 6 | 20 | 75 | R Square | 0.8335 | ||||||
| 7 | Adj R Sq | 0.778 | ||||||||
| 8 | Standard Err | 5.0596 | ||||||||
| 9 | Observations | 5 | ||||||||
| 10 | ||||||||||
| 11 | ANOVA | |||||||||
| 12 | df | SS | MS | F | Significance F | |||||
| 13 | Regression | 1 | 384.4 | 384.4 | 15.0156 | 0.0304 | ||||
| 14 | Residual | 3 | 76.8 | 25.6 | ||||||
| 15 | Total | 4 | 461.2 | |||||||
| 16 | ||||||||||
| 17 | Coefficients | Std Err | t Stat | Pvalue | ||||||
| 18 | (Intercept) | -53.2 | 28.8888 | -1.8415 | 0.1628 | |||||
| 19 | x | 6.2 | 1.6 | 3.875 | 0.0304 | |||||
| 20 |
Lets look at some of these numbers and what they mean. We will use only some of them.
28.3 Interpreting the output of the ToolPak analysis
- Multiple R is 0.913 in E5.
- This is the absolute value of the correlation coefficient, \(R\).
- R Squared is 0.8335 in E6
- This is the square of the correlation coefficient and usually denoted by \(R^2\). This number tells you how scattered the data is. 1.0 means no scatter, and 0.0 means all scatter
- Adjusted R Squared is 0.778 in E7
- This is used for model evaluations in multiple regression. Multiple regression is when you have more than one column of x-variables. Its not useful for simple regression (with one x-variable).
- Standard Error of Estimate is 5.0596 in E8
- This is a error estimate for how far off your predictions might be. It is a typical error you might make when using this model for making predictions.
- Observations is 5 in E9
- This is how many rows of data you have. Its called the sample size sometimes as well.
We will not use all the output from the summary, but we definitely will need two important parts:
- The equation of the regression line (the slope and the intercept)
- The p-value that tells us if the model is significant
The regression equation \(y=mx+b\) is easy to identify from the Coefficients:
- The Intercept is -53.2
- This is the \(b\) in the equation above
- The slope is 6.2
- This is the \(m\) in the equation above
Notice that the slope is next to the name of the x-variable, which in this case is just “x”.
So the regression equation for this situation is this:
\[ y = 6.2x + -53.2 \]
But before we start using this equation we need to see if a linear model is valid. This is what we described in the last section about the signficance of the linear model.
Ultimately this tells us if we should use this equation for predictions or not.
We can determine this by examining the p-value that goes with the overall significance of the linear model.
Locating this is explained in the next section.
28.4 p-value for Overall Significance of the Linear Model
If you examine the output of the regression analysis you will see this in the middle of the output some cells that look like this:
| F | Significance F |
|---|---|
| 15.0156 | 0.0304 |
The thing we want is labeled “Signficance F” in this output. Almost everyone else calls this the “p-value” or the “p-value for the significance of the linear model”. Here it is: 0.0304.
This p-value (if it is small enough) will tell us if there is a significant linear relationship between the y and the x. This notion of a significant linear model was discussed in the last section where we gave a graphical example that used a very small amount of data.
Here is the official test based on the above p-value and how we use it.
28.5 Test of Overall Significance of the Linear Model
- If \(p < .05\), then there is a significant linear relationship between the y and x
- Means it is OK to use the regression equation (if your accuracy allows)
- Means it is OK to use the regression equation (if your accuracy allows)
- If \(p \geq .05\), then there is not a significant linear relationship between the y and x
- Means it is NOT OK to use the regression equation
Since \(p = 0.0304\) and this is less than \(.05\), we conclude there is a significant linear relationship between y and the x. So it makes sense to use the regression equation for predictions.
Now that we know the linear model is significant, lets use the equation to predict y if \(x=6\):
That would be:
\[ y = 6.2x - 53.2= (6.2)(6)-53.2 = -16 \]
Now if the p-value had not been small enough (less than \(.05\)) you would not use the equation for predictions this way. Remember this test is for the validity of using a linear model (a straight line) to model your data. If the linear model is not significant, then you have no business using the equation for predictions.
Keep this in mind, you always need to examine this p-value to make sure you are working with an appropriate model.
28.6 Example Where The Linear Model is Not Significant
Let’s look at the example from a previous chapter where there was just 3 data points.
| temp | gallons |
| 73 | 110 |
| 75 | 97 |
| 77 | 105 |
Here is a scatterplot of this data:

Make sure this data is entered into a spreadsheet in columns A and B of the spreadsheet. Include the names “temp” and “gallons” in the first row as well.
| A | B | C | D | E | F | |
| 1 | temp | gallons | ||||
| 2 | 73 | 110 | ||||
| 3 | 75 | 97 | ||||
| 4 | 77 | 105 | ||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 |
Run the Tookpak add-in and select the linear regression tool. For “Input Y Range” enter in B1:B4 and A1:A4 for “Input X Range”.
You can click on the “Labels” option since you have included row 1 and this contains the labels “temp” and “gallons” for your data.
Now choose D2 as the output cell. This is where your regression summary will go. Go ahead and run the analysis and it should output something like this:
| A | B | C | D | E | F | G | H | I | J | |
| 1 | temp | gallons | ||||||||
| 2 | 73 | 110 | Summary | |||||||
| 3 | 75 | 97 | ||||||||
| 4 | 77 | 105 | Regression | |||||||
| 5 | Multiple R | 0.3812 | ||||||||
| 6 | R Square | 0.1453 | ||||||||
| 7 | Adj R Sq | -0.7093 | ||||||||
| 8 | Standard Err | 8.5732 | ||||||||
| 9 | Observations | 3 | ||||||||
| 10 | ||||||||||
| 11 | ANOVA | |||||||||
| 12 | df | SS | MS | F | Significance F | |||||
| 13 | Regression | 1 | 12.5 | 12.5 | 0.1701 | 0.751 | ||||
| 14 | Residual | 1 | 73.5 | 73.5 | ||||||
| 15 | Total | 2 | 86 | |||||||
| 16 | ||||||||||
| 17 | Coefficients | Std Err | t Stat | Pvalue | ||||||
| 18 | (Intercept) | 197.75 | 227.3855 | 0.8697 | 0.5443 | |||||
| 19 | temp | -1.25 | 3.0311 | -0.4124 | 0.751 | |||||
| 20 |
In this case the p-value for the significance of the model is given in I13 and the value is \(0.7509899\). Since this is bigger then \(.05\), the is not a significant linear relationship between \(temp\) and \(gallons\).
So this means we should NOT use the regression equation here to make predictions.
We have already seen that in fact the regression equation doesn't make sense once we include more of the data. The slope of the relationship here should be positive since as \(temp\) goes up it is likely that \(gallons\) would go up as well since this is gallons sold.